高中数学求解几何体积的方法

　　同学们，我们上一篇文章讲了一下三视图最高效还原方法：拔高法，那么今天我们来讲一下终极结论一：由三视图求锥体体积。

　　同学们三视图这类题型有百分之90可以用拔高法还原，有百分之10的题型要用正方体切来还原，同们学做题的时候首选拔高法，因为拔高最高效，在用不了拔高法的题型采用正方体切，那么哪些题要用正方体切，同学们注意了三视图有三种题型，看下图：

　　三视图求体积如果是组合体问题，你只需要把三视图还原完就可以轻松解决了。由于这种题目灵活度比较高，比如说它的底座俯视图、外轮廊是三角形或四边形也好，只要上顶点稍微左右前后移动，那么这个三视图将会产生实质变化，所以，它出现在高考里边就比较频繁一些。

　　告诉大家综合运算在高考考察的频率是最高的，还原完三视图以后是让同学们读出最长棱长和面积的最大值或者求体积表面积;求体积表面积是经常考察的是锥体的题型;为什么锥体考察频率最高了?就是因为如果你的底面是三角形也好、四边形也好你的上顶点稍微前后左右平动一些，这个立体图形的三视图会发生本质上的改变;所以锥体求体积、表面积这种题型出现的频率最高。今天老师给大家讲的是只要有关锥体体积、表面积都可以做到秒杀。

　　由三视图求锥体体积，你如果用常规运算三五分钟做不来的题目，只要用到我们今天讲的终极结论一，是可以10几秒解决掉的。

　　一、首先，请大家先记住并理解这三句话，这是三视图所具有的特征：

　　①长对正：正视和俯视长度相等;

　　②高平齐：正视和侧视高度相等;

　　③宽相等：侧视和俯视宽度相等。

　　二、终极结论一结论：

　　当三视图有2个视图外轮廊为三角形时，则得到体积公式：V=1/3*S(第三)*h(两同)。

　　①h(两同)是指： 3个视图有2个视图外轮廊为三角形。然后看它们是什么相等关系，请回顾上面三句话：长对正，高平齐，宽相等。

　　②S(第三)是指：第三个视图的面积。

　　下面我们就以讲解题的方式，帮助大家进一步理解并掌握这个方法!

　　大家可以看到，第一题这道题的正视图和侧视图外轮廊为三角形的，那我们就得到它们的度高相等，就是h(两同)。S(第三)就是另外一个视图的面积。我们就根据体积公式，就非常迅速地算出此四棱锥的体积了，看下图：

　　大家就可以看到，是不是就这样秒掉了!用这样的方法解题非常迅速、非常暴力!

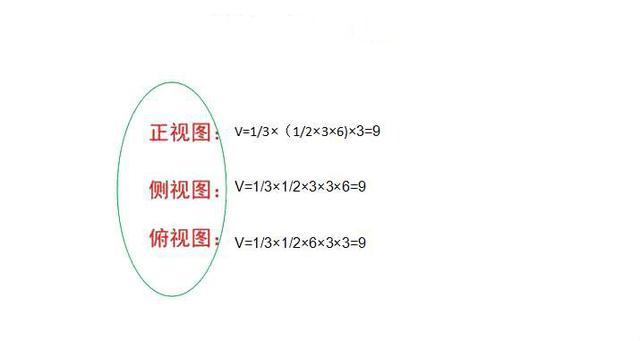
　　好，下面再看第二题，大家发现这三个视图都是三角形，那么我们可以把任何一个视图看成S(第三)，如果大家不信，我们可以一一验证，算出来的结果肯定都是一样的!看图：

　　继续看第三题，很明显正视图和侧视图两个外轮廓为三角形，就是我们所说的h(两同)，那么俯视图就是我们所说的的S(第三)，则直接可以求出体积：

　　第四、第五、第六、第七、第八、第九、第十题同理迅速出答案，我就不一一做解题了，留给大家练习。

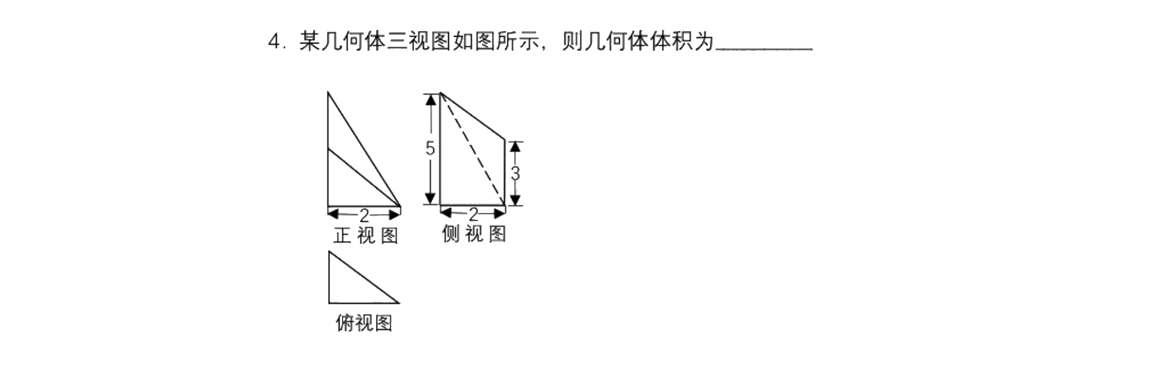
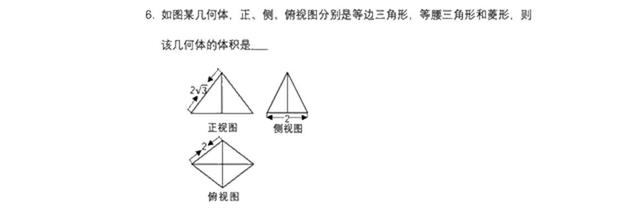
　　那再看第十一、十二题应该怎么做，我告诉大家，这两题不能用拔高法，不能用终极结论一，而是要用六字真言才能解决，这是一眼都能看出来的，你们看出来了吗?

　　那么，哪些题型可以用拔高法，哪些题可以终极结论一，哪些题才能用六字真言才能完美解决呢?欢迎留言讨论，针对这篇文章如果还有看不明白的地方，也可以私信获取这篇文章的完整视频。欢迎大家关注并留言。