公元1858年,德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:
把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。
这种纸带被称为“莫比乌斯带”(也就是说,它的曲面只有一个)。
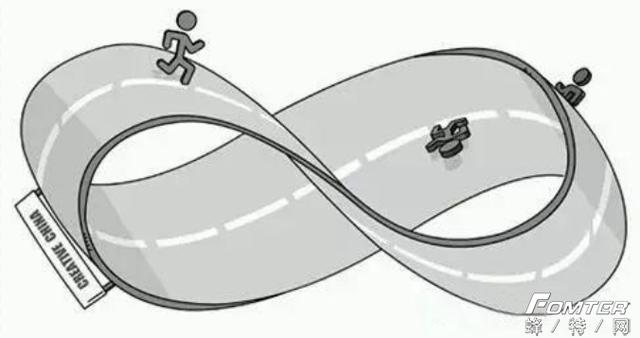
小编是在小学的时候,看到一本叫做《数学十万个为什么》的书上介绍了这个东西,于是当时真的做了这个纸环,并抓了只虫让它在上面爬……
然鹅,那只虫并没有想象中那么听话……
这次偶然又想起这个事,为了切实体验一把虫子是如何在一个只有一个面的世界上爬,小编做了下面的东西,诺~
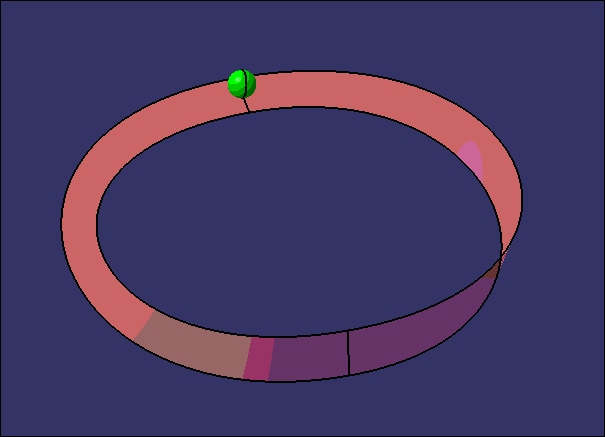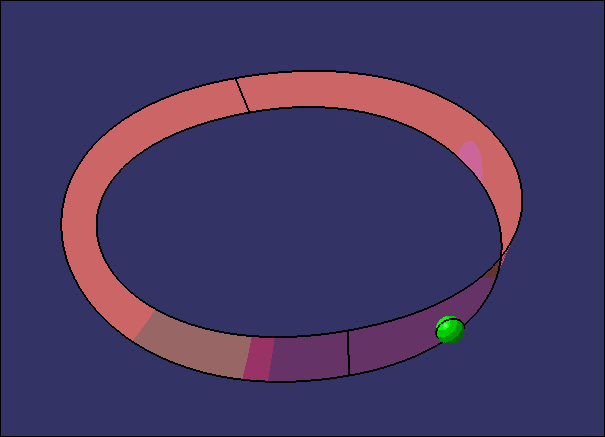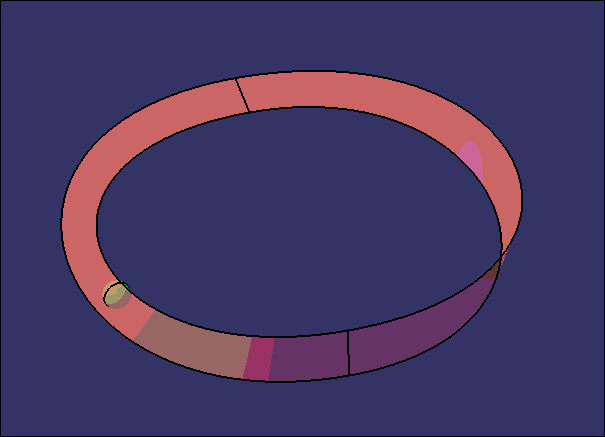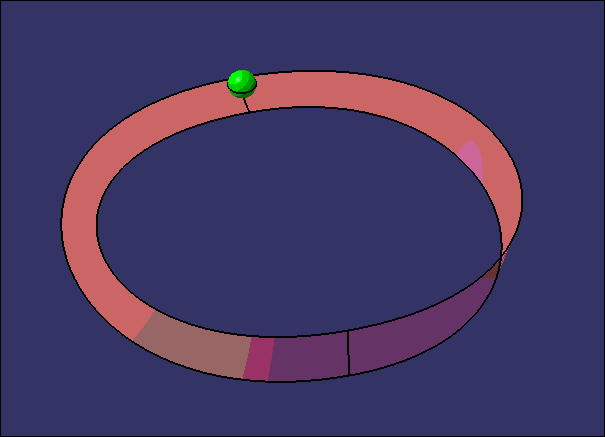
不过呢,大家看到的这个环形并不是1个曲面而是2个,在CATIA中这两个曲面是会报错的。
至于具体的DMU怎么做的,在这里就不做具体的叙述了。相信各位看了下面的特征树及辅助线就一目了然了~
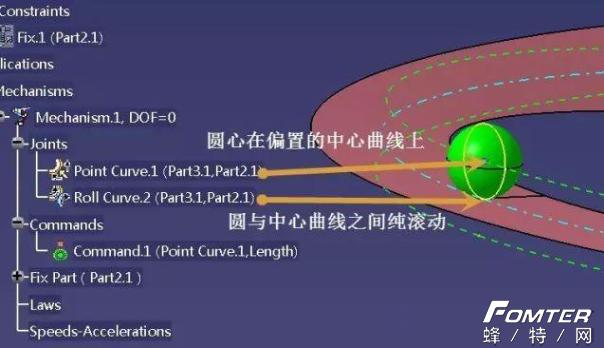

就像小编在本文标题中说的,做这个东西除了能直观地观察莫比乌斯环之外,并没有什么意义。如果非要说有什么用的话,那就是能练习一下DMU中的运动副的使用吧,或者说如何用较少的限制做这种小球滚动的运动仿真。比如说,是不是可以用同样的方法做出下面这个运动捏~
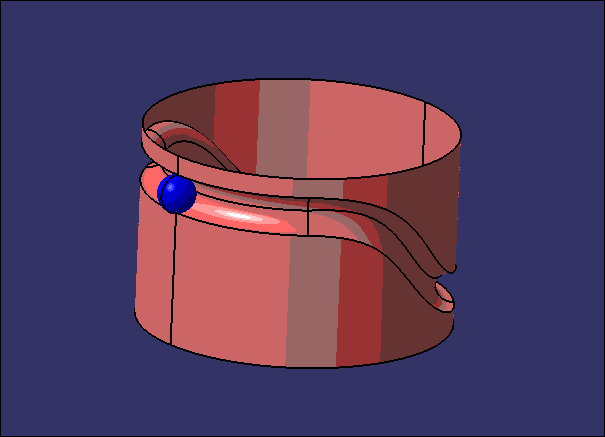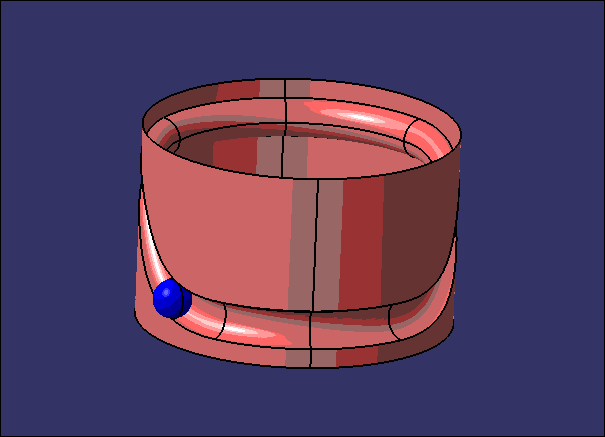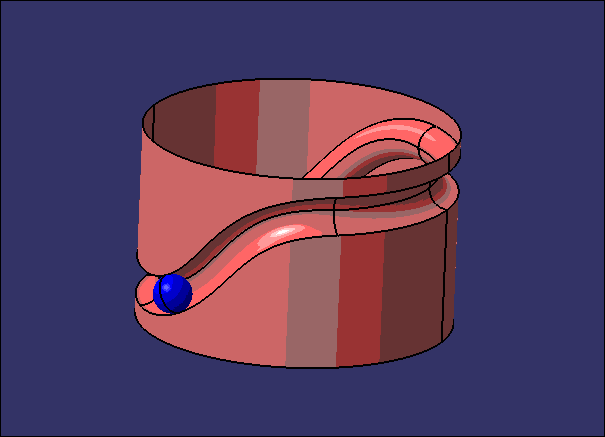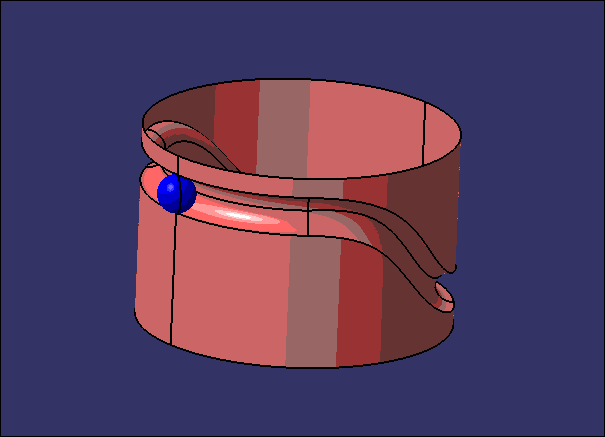
〖特别声明〗:本文内容仅供参考,不做权威认证,如若验证其真实性,请咨询相关权威专业人士。如有侵犯您的原创版权或者图片、等版权权利请告知 wzz#tom.com,我们将尽快删除相关内容。

 微信扫一扫
微信扫一扫