全等的基本模型练习题

在解决几何问题中，“一线三等角，K形全等”的基本图形常常出现，我们称之为“三垂直模型”，掌握好该模型及其变形，有助于我们解决复杂几何数学题。

“三垂直模型”的一般形式：

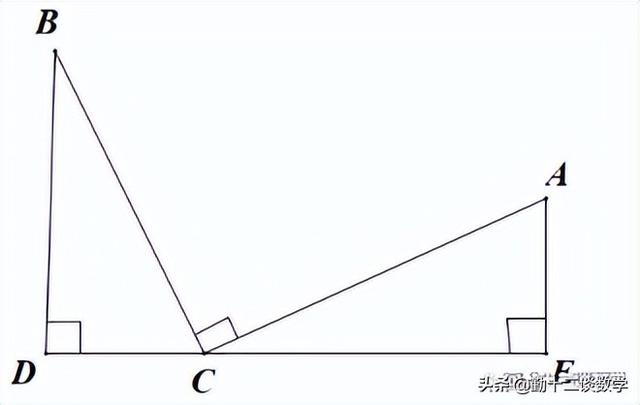
这是最基础的“三垂直模型”，在同一直线上有三个直角，即∠D=∠ACB=∠E，且BC=AC，那么可以通过“AAS”或“AAS”判定两个三角形全等。两个三角形已经满足两个条件，加上∠B ∠BCD=90°，∠BCD ∠ACE=90°，所以得到∠B=∠ACE，那么通过“AAS”得到△BDC≌△CEA。

其它“三垂直模型”：

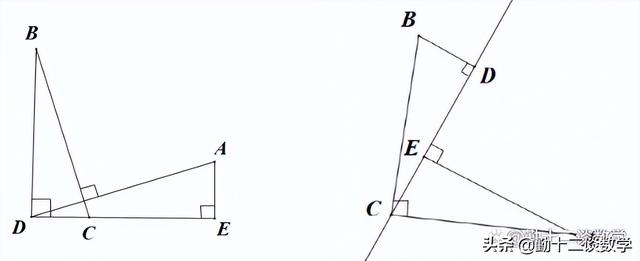
证明的方法与上面类似，通过直角三角形两个锐角互余，得到两个角相等，从而证明两个三角形全等。

例题1：如图，∠ACB=90°，AC=BC，AE⊥CE于点E，BD⊥CD于点D，AE=5cm，BD=2cm，求DE的长

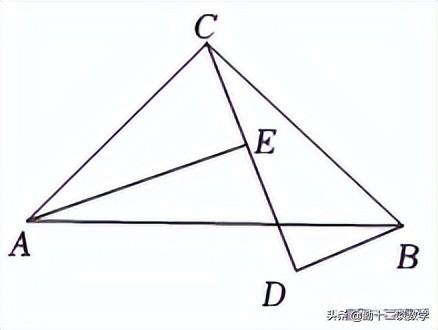
分析：看到等腰直角三角形，我们应该可以想到很多结论，比如“三线合一”，比如在等腰直角三角形的斜边中点处构造直角与两腰相交，会得到一个新的等腰直角三角形等等。

并且，等腰直角三角形满足一个角为直角，且两条腰相等，因此我们也常构造“三垂直”模型，过顶点的一条直线绕着顶点旋转，过两个底角顶点做该直线的垂线，可以构造出“三垂直模型”，有“内K图”，也有“外K图”。

本题可根据AAS证明△ACE≌△CBD，可得AE=CD=5cm，CE=BD=2cm，由此即可解决问题。

本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形解决问题。

例题2：如图，在△ABC中，∠ACB=90°，AC=6，BC=8，以斜边AB为边向外作正方形ABDE，连接CE，求CE的长

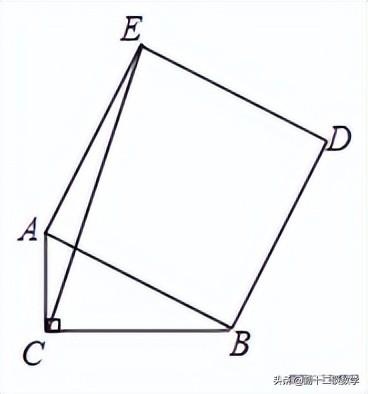
分析：延长AC，过E作EF⊥AF，垂足为F，由ABDE为正方形，利用正方形的性质得到一对角为直角，AE=AB，利用同角的余角相等得到一对角相等，再由一对直角相等，利用AAS得到三角形AEF与三角形ABC全等，利用全等三角形的对应边相等得到EF=AC=6，AF=BC=8，由FA AC求出FC的长，在直角三角形CEF中，利用勾股定理即可求出EC的长．

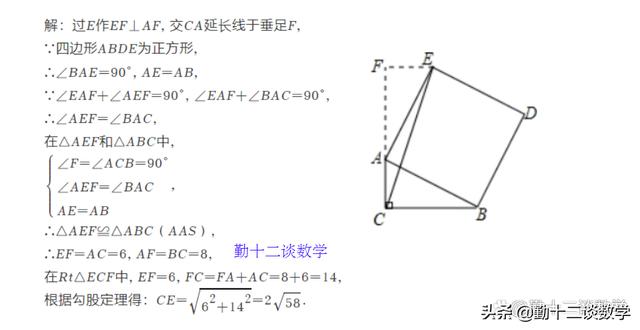
此题考查了勾股定理，正方形的性质，以及全等三角形的判定与性质，熟练掌握勾股定理是解本题的关键。

通过这两题可以发现，如果出现等腰直角三角形或者正方形时，我们可以试着构造”三垂直模型“得到全等三角形，从而进行解题。