高中数学第一章集合与逻辑用语

一、集合

集合的概念

集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体。其中，构成集合的这些对象则称为该集合的元素。

集合用大括号或大些字母表示，元素通常用小写字母表示。

集合的特性

1.确定性

给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现。

如“世界最高的山”可表示集合，“著名作家”、“高一较难的题”不表示集合。

2.互异性

一个给定集合中的元素是唯一的，不可重复的，每个元素只能出现一次。根据这一特性可以区分数列(元素可重复出现)和集合。

如{1，0，a}表示一个集合，则a≠1且a≠0。

3.无序性

一个集合中，每个元素的地位都是相同的，元素之间是无序的。

如{a b c}和{a c b}表示同一集合。

集合的表示

1.列举法

把集合中的元素一一列举出来，基本形式是{a b c d …}。

2.描述法

用确定的条件表示某些对象是否属于这个集合，基本形式是{x|P(x)}。

3.图像法

图像法，又称韦恩图法、韦氏图法，是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合，是集合的一种直观的图形表示法

4.符号法

有些集合可以用一些特殊符号表示。

N：非负整数集合或自然数集合{0 1 2 3 …}

N*或N ：正整数集合{1 2 3 …}

Z：整数集合{… -1 0 1 …}

Q：有理数集合

Q ：正有理数集合

Q-：负有理数集合

R：实数集合(包括有理数和无理数）

R ：正实数集合

R-：负实数集合

C：复数集合

∅ ：空集（不含有任何元素的集合）

集合的分类

1.空集

空集是不包含任何元素的集合，记为∅。

2.有限集

含有有限个元素的集合叫做有限集。

3.无限集

含有无限个元素的集合叫做无限集。

元素与集合的关系

元素a与一个给定的集合A只有两种可能：

1、a属于集合A，表述为a是集合A的元素，记作a∈A。

2、a不属于集合A，表述为a不是集合A的元素，记作a∉A。

集合与集合的关系

子集

如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集，记为A⊆B或 B⊇A，读作“集合A包含于集合B”或“集合B包含集合A”。

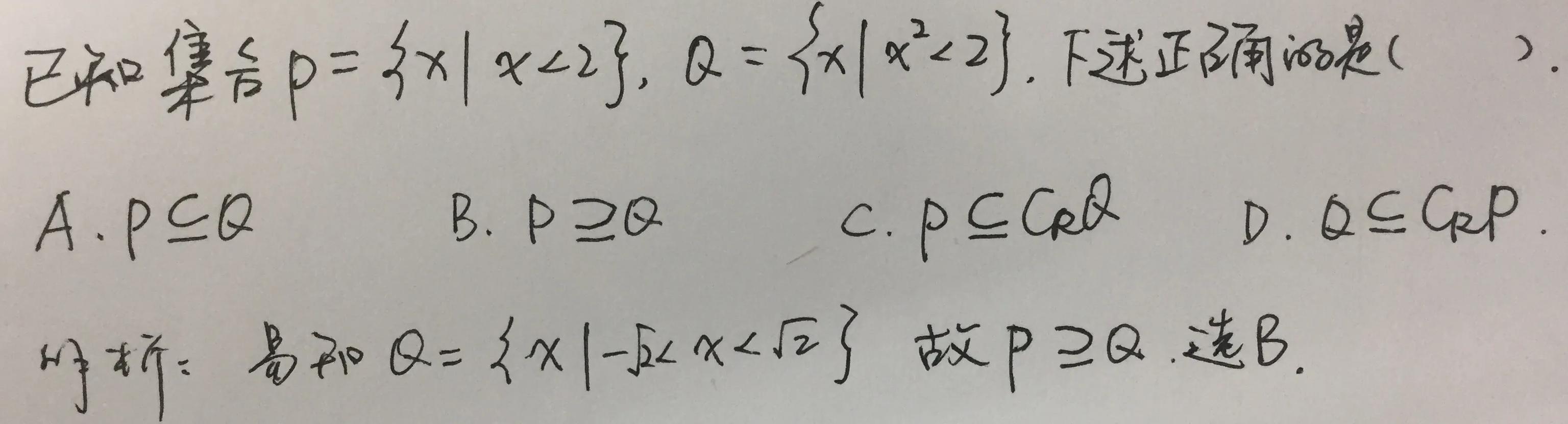
真子集

若集合A是B的子集，存在元素x属于B但不属于A，则称集合A是集合B的真子集。

空集是任意一个非空集合的真子集，是任何一个集合的子集。

集合间的基本运算

交集

由属于集合A且属于集合B的元素所组成的集合，叫做集合A与B的交集．交集A∩B＝{x|x∈A且x∈B}。

并集

由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集．并集A∪B＝{x|x∈A或x∈B}。

全集

在研究集合与集合之间的关系时 这些集合往往是某个给定集合的子集 这个确定的集合叫做全集，全集通常用U表示。

补集

设U是一个集合 A是U的一个子集 由U中所有不属于A的元素组成的集合 叫做U中子集A的补集(或余集)记作CuA。

常用性质

并集的性质：

（1）A⊆A∪B，B⊆A∪B，A∪A=A，A∪∅

=A，A∪B=B∪A。

（2）若A∪B=B，则A⊆B，反之也成立。

交集的性质：

（1）A∩B⊆A，A∩B⊆B，A∩A=A，A∩

∅=∅ A∩B=B∩A。

（2）若A∩B=A，则A⊆B，反之也成立。

二、常用逻辑用语

命题

1.命题的概念

在数学中用语言、符号或式子表达的，可以判断真假的陈述句叫做命题。

命题包含两部分：题设和结论。判断为真的语句叫做真命题，判断为假的语句叫做假命题。

如：若a>0，则a 2>0，是真命题。

2.四种命题

原命题：若p，则q。

逆命题：若q，则p。

否命题：若¬p，则¬q。

逆否命题：若¬q，则¬p。

真假关系：

两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系。

充分条件和必要条件

1、定义

如果p⇒q，则p是q的充分条件，q是p的必要条件。

如果p⇒q，q⇒p，则p是q的充要条件。

2、充要条件判断

例题：

简单的逻辑联结词

命题中的“且”“或”“非”叫做逻辑联结词。

用联结词“且”联结命题p和命题q，记作p∧q，读作“p且q”。

用联结词“或”联结命题p和命题q，记作p∨q，读作“p或q”。

对一个命题p全盘否定，就得到一个新命题，记作¬p，读作“非p”或“p的否定”。命题p和¬p是完全对立的，有且只有一个成立。

简单复合命题的真值表：

例：若命题“p∧q”为假，且“¬p”为假，则（ ）

A．p或q为假

B．q假

C．q真

D．不能判断q的真假

解析：由于“p∧q”为假，故p和q不会都为真；又有“¬p”为假，则p为真。所以有p为真q为假，p或q为真。答案为B。

量词

全称量词与存在量词

(1)包括全体的量词叫做全称量词，常见的全称量词有：“任意”“一切”“所有”“全部”等，用符号“∀”表示。

(2)只含有一部分的量词叫做存在量词，常见的存在量词有：“存在”“至少有一个”“有些”““某个”“有的”等，用符号“∃”表示。

全称命题与特称命题

(1)含有全称量词的命题叫全称命题: “对M中任意一个x，有p(x)成立”可用符号简记为∀x∈M，p(x)，读作“对任意x属于M，有p(x)成立”。

(2)含有存在量词的命题叫特称命题: “存在M中的一个x，使p(x)成立”可用符号简记为∃x∈M，P(x)，读作“存在元素x属于M，使p(x)成立”。

命题的否定

(1)含有量词命题的否定

全称命题p：∀x∈M p(x)的否定¬p为：

∃x∈M ¬p(x)；全称命题的否定为存在命题。

存在命题p：∃x∈M p(x)的否定¬p：∀x∈M ¬p(x)；存在命题的否定为全称命题。

其中p(x)是一个关于x的命题。

(2)含有逻辑连接词命题的否定

“p或q ”的否定：“¬p且¬q”；

“p且q ”的否定：“¬p或¬q”

(3)“若p则q”命题的否定：只否定结论

命题的否定只否定结论；否命题是题设和结论全否。

对命题p的否定（即非p）是否定命题p所作的判断，而“否命题”是 “若¬p则¬q ”。

例1：原命题：若a>0，则a 1>0。

命题的否定：存在a>0，有a 1≤0。

否命题：若a≤0，则a 1≤0。

例2：原命题：等腰三角形底角相等。

命题的否定：等腰三角形底角不相等。

否命题：若三角形不是等腰三角形，则他们的底角不相等。